If a trie falls in the forest...

…does it raise an exception?

A trie is one of those fancy data structures you may have heard peers at work throw around in discourse at the coffee machine. Or maybe you’re interviewing at a FAANG. Or you like LeetCode. Regardless, there’s no need to feel intimidated; a trie is just a tree! I love how easy that is to remember. I’ve also seen it pronounced as “try”, but I like the other origin better: a tree used for fast retrieval. The most popular use case I’ve seen for it is to compare similar strings. For example: spell checking, auto-completion, or language filtering.

The trie in all its glory

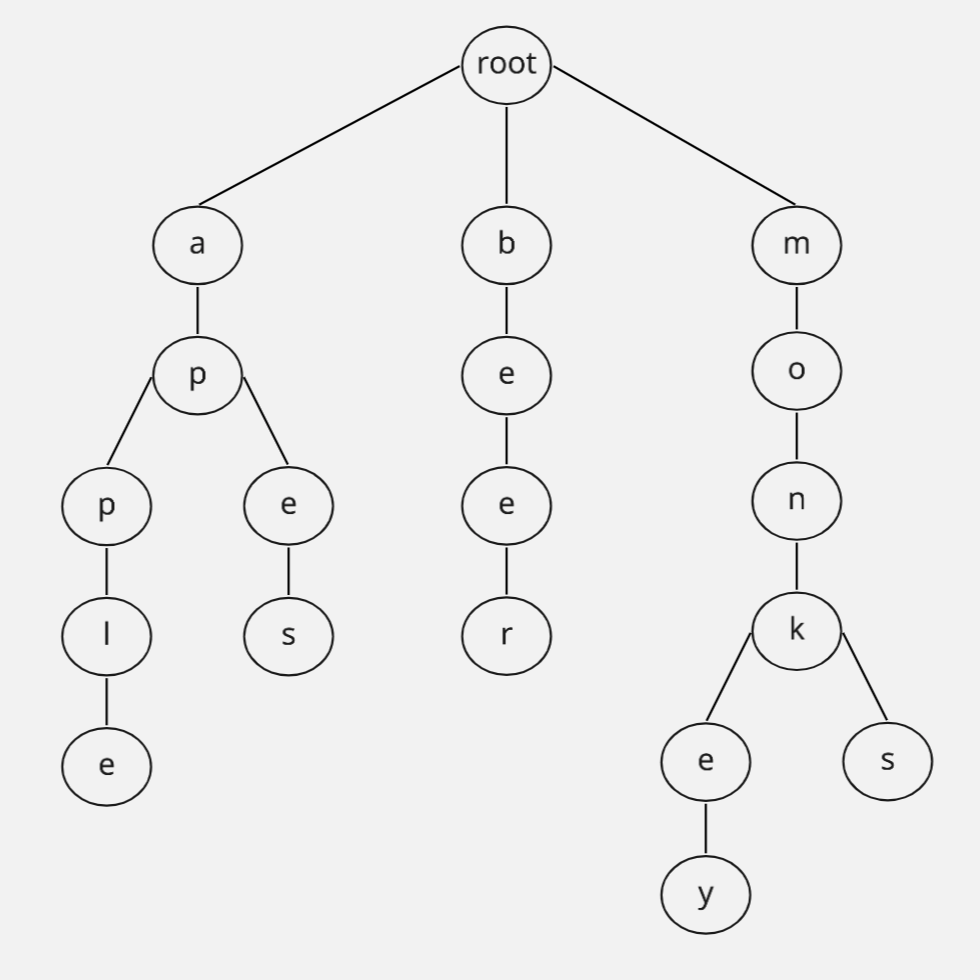
Say I start typing “ap” in a text box that provides auto-completion. Searching the trie above for those letters would show me that “apple” and “apes” are the only possible words that can come next. The trie acts as a source of truth, like a dictionary. Another use is searching strings for exact matches. Maybe I want to scan for potty mouth words (shit) and their l33t versions ($h1t). All you have to do is build up a trie and search it. Let’s do it!

The plan

First, we need to think of how to model a trie in code. A trie is most commonly represented as a node pointing to an array of child nodes (no binary trees allowed here). However, this seems inefficient. On every search, each array of child nodes would need to be searched all over again. Is there a way to avoid this O(n) cost for every child collection? Maybe even get an O(1) operation? By George, there is! The map (or hash, dictionary, associative array; wherever you’re from).

Using our example trie from above, instead of a node pointing to an array of nodes:

root -> [a -> [p -> [p -> [l -> [e]], e -> [s]]]]

we could say a node is a map of breadth-level values pointing to other nodes.

    {a,    b,  m}    - 1 map
     |     |   |
    {p}   {e} {o}    - 3 maps
     |     |   |
  {p,  e} {e} {n}    - 3 maps
   |   |   |   |
  {l} {s} {r} {k}    - 4 maps
   |           |
  {e}       {e,  s}  - 2 maps
             |
            {y}      - 1 map

Essentially, when a letter branches, it points to a single map with the keys being all child letters and their values being more maps. This actually allows us to do away with a root node entirely, and provides O(1) access to a node’s children. It’s also extremely recursion friendly. And so is Elixir, which is what we’re going to use to build this bad boy.

The c0d3

Before we can search our trie, we have to populate it. How should we do that? Let’s figure out how the code is going to be used before actually writing it. Finding the interface to structures and algorithms tends to help drive their implementation. One way to build a trie is to add a word at a time:

trie =
  Trie.new()
  |> Trie.insert("apple")
  |> Trie.insert("apes")
  |> Trie.insert("beer")
  |> Trie.insert("monkey")
  |> Trie.insert("monks")

I like it. Let’s go over those two functions in the Trie module, new and insert:

defmodule Trie do
  def new, do: %{}
end

There’s our root node; a humble empty map. Now for the easy function:

def insert(trie, word) do
  insert_graphemes(trie, String.graphemes(word))
end

Our interface function breaks up the word string into a list of Unicode graphemes before passing it to the workhorse. If you’ve never heard of a grapheme, you’re not alone. It’s essentially a character, and it can consist of multiple code points.

defp insert_graphemes(trie, [grapheme | rest]) do
  subtrie =
    Map.get(trie, grapheme, %{})
    |> insert_graphemes(rest)

  Map.put(trie, grapheme, subtrie)
end

defp insert_graphemes(trie, []), do: trie

This recursion can be a little mind bending for the uninitiated. Let’s take "apple" as our word; this makes the grapheme list ["a", "p", "p", "l", "e"]. On first application, the "a" is split from the list. Next, the trie is accessed to see if "a" has a map of children (it doesn’t yet). An empty map is returned as default, and the rest of the graphemes are inserted into this map recursively, with the process starting again for "p". Finally, this subtrie is inserted into the trie under the "a" key where it all began.

Let’s understand the base case when the second argument is an empty list. The grapheme will be "e" and rest will be []. At this point, the trie is still an empty hash since this entire function has yet to return and resolve the recursion. Therefore, when the base case is reached, the empty map is returned, bound to the subtrie, and "e" ends up pointing to this empty map. Here’s a visual of the callstack and final data:

insert_graphemes(%{}, ["a" | ["p", "p", "l", "e"]])
insert_graphemes(%{}, ["p" | ["p", "l", "e"]])
insert_graphemes(%{}, ["p" | ["l", "e"]])
insert_graphemes(%{}, ["l" | ["e"]])
insert_graphemes(%{}, ["e" | []])
insert_graphemes(%{}, [])

%{"a" => %{"p" => %{"p" => %{"l" => %{"e" => %{}}}}}}

When we insert “apes” next, "a" now points to a map, and “pes” will be recursively inserted into it with the resulting trie being:

%{"a" =>
  %{"p" =>
    %{
      "p" => %{"l" => %{"e" => %{}}},
      "e" => %{"s" => %{}}
    },
  }
}

Beautiful! We’ve implemented our interface and constructed a trie! Now what do we do with it? Let’s use it as a potty mouth catcher. Maybe we are running a chat server and want to filter out swear words and their leet code counterparts. We come across “$h1t”. Is it bad? Ask the trie.

bad_words = %{"$" => %{"h" => %{"1" => %{"t" => %{}}}}}
Trie.exists?(bad_words, "$h1t") => true

GASP! I knew it. But how does it work?

def exists?(trie, word) do
  search_graphemes(trie, String.graphemes(word))
end

Once again, break the word into graphemes first.

defp search_graphemes(trie, [grapheme | rest]), do: search_graphemes(trie[grapheme], rest)
defp search_graphemes(trie, []) when trie == %{}, do: true
defp search_graphemes(_, _), do: false

Oh man, Elixir is slick. One line for each method thanks to function signature pattern matching. We take the first grapheme and access its subtrie. Rinse and repeat for the rest of the graphemes in the word. If the full word matches, then we’ll end up with an empty map and empty list and return true all the way up the callstack (except we have no callstack because our tail calls are optimized! sick). Otherwise, after the graphemes run out and the trie is not exhausted, we return false because it’s not an exact match. And that’s how you search a trie for our use case!

Final Summation

I was surpised how succinctly a trie can be constructed and searched when implemented with recursion. Don’t be intimidated by the arcane data structures that FAANG companies expect you to know by heart. Some of them serve niche practical use cases, but at the end of the day, they are just neat ways to store values.